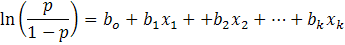
In my previous article on the success of 3NT when the high cards are split unevenly, I found that 4HCP opposite 21HCP makes game only about 47% of the time, compared with 59% for 25 HCP divided approximately evenly. I speculated that the cause was lack of entries to dummy to make directed leads, and that what we really wanted was a rule that said "raise to 3 if we have a likely entry", rather than a rule saying "raise if you have X HCP."
As a step toward answering that question, I analyzed a pool of hands where both North and South were dealt balanced or semibalanced hands; South had 20 or 21 HCP; and no 8-card spade or heart fit existed. I then recorded which deals could make 3NT and which couldn't, along with high-card and distributional information about North's hand.
I then subjected the data to a statistical technique called logistic regression, which models the probability of success (making at least nine tricks in notrump) as a function of one or more explanatory variables. The "line" of best fit is an S-shaped curve, reflecting the fact that with subminimum values game is almost certain to fail; with excessive values game is almost certain to make (regardless of what exactly those values are); while in a critical intermediate zone, a small change in assets can produce a large change in the chance of making 3NT. Mathematically, the model has this form:
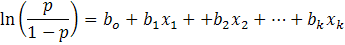
My hypothesis was that one ace should be worth much more than two queens or four jacks; an ace is a certain entry to dummy, and a king is a likely entry. It is also commonly believed that a 5-card suit is an asset for notrump play, so I also used the length of dummy's longest suit (actually, length in excess of 4) an additional explanatory variable. That is, my first model was
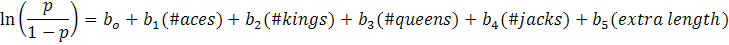
If standard HCP evaluation is correct, b1 should be about four times b4.
Perhaps surprisingly, the effect of having a 5-card suit in dummy was not statistically significant. (I expect this is because it is relatively rare to run dummy's weak 5-card suit when dummy entries are short.) The coefficients for the equation of best fit with their standard errors were:
As expected, we see that aces and kings are substantially more valuable here (4.7 : 3.6 : 2.2 : 1) than the standard 4:3:2:1 HCP ratio suggests. Proposing hand evaluation methods where the Ace:Jack ratio higher than 4:1 is very common; but a ratio as high as 4.7:1 is unusual, as is the finding that a queen is significantly more than twice as valuable than two jacks.
The probability of success needed to justify bidding 3NT is 50% at matchpoints, about 40% not vulnerable at IMPs, and about 33% vulnerable at IMPs. (See my previous article for an explanation of why 40% and 33% are adequate rather than the usual 44% and 41%.) These correspond to "log odds," ln(p/(1-p), of 0, -0.41, and -0.71, respectively. We can plug these values into our equation and rearrange it into a more digestible form:
Bid game if 4.7 x (Aces) + 3.6 x (Kings) + 2.2 x (Queens) + Jacks is at least...
Since we're talking about such weak hands, it is easier to list the relevant card combinations than to remember a formula with decimals:
![[Plot of logistic curve]](raise2n_curve.png)
To test our model we can generate some additional hands where responder holds the critical 4- and 5-HCP holdings and see how closely the results agree with our predictions:
| Dummy's holding: | Predicted success rate | Results of test simulation |
|---|---|---|
| K+Q | 59.7±2.6% | 598/1000 |
| A+J | 58.0±3.0% | 582/1000 |
| KJJ | 55.6±2.9% | 572/1000 |
| QJJJ | 48.7±4.0% | 1497/3000 ~ 49.9±1.8% |
| A | 39.6±3.3% | 1840/5000 ~ 36.8±1.3% |
| K+J | 37.3±2.4% | 1851/5000 ~ 37.0±1.3% |
| Q+Q | 34.7±3.3% | 1890/5000 ~ 37.8±1.3% |
| QJJ | 31.1±2.4% | 312/1000 |
| JJJJ | 27.7±4.7% | 293/1000 |
(I ran 1000 hands for each case, plus extra hands as needed for those deals very close to the break-even points. Uncertainties for the simulations (95% confidence level) are ±3% for n=1000.)
I confess I am a little disappointed in the results: though ace- and king-rich holdings are better than 'quacks', the model substantially overstated the size of the difference, and reached one incorrect conclusion (predicting QQ was worse than A or KJ.) Apparently with such a strong balanced opener, queens are likely enough to be entries that two queens is quite a valuable holding. At matchpoints and NV IMPs, "raise with any 5, pass with any 4" looks like pretty good advice after all. Vulnerable at IMPs, any 4 not including two jacks.
The above still does not capture the fact that KQ in the same suit is a nearly certain entry while a king and queen in two different suits are less certain. We could handle this by explicitly adding KQ and KJ honour combinations into the model as two extra variables; or, more simply, by using just two explanatory variables, HCP and Quick Tricks. (Remember from your 1950s Goren: AK = 2, AQ = 1½, A or KQ = 1; K = ½.)
A quick additional simulation finds that, while honours in combination are more valuable than apart, the difference is not usually enough to change responder's decision, except for raising with KJ only in combination, NV at IMPs:
| Dummy's holding: | Results of test simulation: |
|---|---|
| KQ together | 587/1000 |
| KQ apart | 582/1000 |
| KJJ together | 603/1000 |
| KJJ apart | 559/1000 |
| KJ together | 422/1000 |
| KJ apart | 369/1000 |
Nothing earthshattering here, but I will report these anyway for the benefit of people who are scared of any kind of regression other than linear. We saw previously that we expect to gain about 0.5 tricks for each HCP in responder's hand. We can test here whether that translates directly into 2 tricks per ace, 1.5 per king, and 1 per queen or not. The line of best fit was
The uncertainties were about ±.03 at the 95% confidence level for all four slopes. We see the same 4.7 : 3.6 : 2.2 : 1 ratio we saw in the logistic regression.
This equation doesn't directly predict our chances of making 3NT, but we might reasonably estimate that if the expected number of tricks is over 8.5, we are likely to have a 50% chance at game. Using this rule of thumb, the linear model says we should raise to 3NT with any 5HCP except QJJJ which is right on the cusp — essentially identical to the results of our more complicated analysis above.